Convertendo imagens em 16 cores no MSX – parte 1

Após escrever sobre como usar Python para converter imagens para o modo de 256 cores do MSX2 resolvi experimentar também a conversão para 16 cores. Motivo? Pura curiosidade de saber como a coisa é feita. Pesquisei um pouco, escrevi algumas linhas de código, obtive resultados interessantes e então fiquei algum tempo sem tocar no assunto.

Ao revisitar notei que não lembrava como tudo aquilo funcionava e decidi fazer duas coisas: (1) analisar o código para entender o que estava acontecendo e (2) escrever isto aqui para não precisar fazê-lo outra vez! 😀

E, como ficou maior do que eu esperava, resolvi separar em duas partes com esta primeira contendo um pouco de teoria e os passos necessários para a conversão da imagem em si…

Os modos de 16 cores do V9938

O V9938, o processador de vídeo do MSX2, possui dois modos de vídeo que exibem até 16 cores¹, um de 256 e outro de 512 pixels de largura e ambos com 192/212 linhas cada (ou 384/424 em modo entrelaçado). Mas diferente do modo com 256 cores, aqui a VRAM não armazena a cor em si mas o índice de uma tabela contendo a cor a utilizar naquele pixel. Por este motivo estes modos de vídeo são chamados de indexados.

Ao todo são 16 índices², cada qual contendo o valor de cor em RGB armazenado em 2 byte e não sendo mais necessário fazê-la caber em 8 bits (o caso do modo de 256 cores), todas as 512 cores da paleta de 9 bits encontram-se disponíveis para uso e assim o cubo RGB torna-se realmente um cubo.

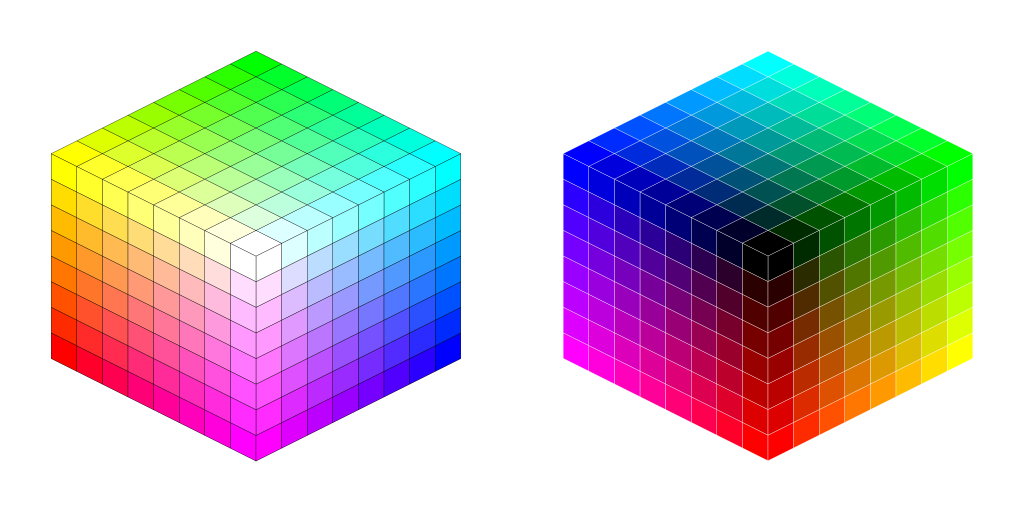
Cada byte da VRAM armazena os índices de dois pixels vizinhos, os 4 bits mais significativos (do lado esquerdo, bits 7, 6, 5 e 4) representando as colunas pares enquanto que os 4 menos significativos (do lado direito, bits 3, 2, 1 e 0) os ímpares, ou seja:

byte da VRAM = índice da coluna par × 16 + índice coluna ímpar

Para calcular o endereço de cada pixel, usa-se:

endereço da VRAM = posição Y × (largura ÷ 2) + posição X

Assim o modo de vídeo de 256×192 consome 24.576 bytes da VRAM (256×192÷2), enquanto que o de 512×192 o dobro, ou seja, 49.152 bytes (512×192÷2) sendo possível armazenar até 4 e 2 páginas de vídeo, respectivamente nos 128 KiB de VRAM disponíveis para o VDP usar.

E, claro, neles também linhas pares e ímpares ficam cada uma em uma página de vídeo quando usando o modo entrelaçado… 🙂

(¹) o MSX2 tem ainda um modo de vídeo de 4 cores com 512 pixels de largura onde cada conjunto de dois bits apontam para um valor de cor na tabela de cores.

(²) No caso do modo de 4 cores, uma tabela menor de apenas quatro índices.

Imagem de exemplo

Para testar a rotina de conversão, separei (cuidadosamente) uma imagem e a redimensionei para o tamanho da tela do MSX, ou seja, 256×192 pixels.

E mais uma vez trabalharei com 192 linhas para manter o aspecto de 4:3 da tela.

Frequência de cores

Tecnicamente o processo de conversão de uma imagem para 16 cores é igual ao de conversão das imagens de 256 cores, ou seja:

1. Ler a cor do pixel;
2. Selecionar a cor mais próxima nas cores disponíveis e
3. fazer a substituição.

A diferença principal está no fato de que para o modo de 256 cores está disponível uma paleta de cores contendo a metade das combinações possíveis de cores com uma resolução de 9-bits, isto é, quase todas as cores necessárias estão presentes.

Mas em 16 cores não, pode-se até usar uma paleta genérica mas para se obter um resultado realmente satisfatório é necessário construir a “melhor paleta de cores possível para aquela imagem” e para tal é preciso primeiro saber quais as cores presentes na imagem e a frequência que se repetem.

Cálculo da frequência das cores

Começando com uma função para calcular a frequência de cores (em “functions.py”):

color_value = lambda color: color[1]

def count_colors(image):

    bitmap = image.load()
    colors = {}

    for y in range(image.height):
        for x in range(image.width):
            r, g, b, *__ = bitmap[x, y]
            r &= 0xe0
            g &= 0xe0
            b &= 0xe0

            colors[(r, g, b)] = colors.get((r, g, b), 1) + 1

    return [(k, v) for k, v in colors.items()]

O que a função faz é varrer a imagem pixel a pixel, reduzir a resolução para 9-bit do MSX, somar cada cor encontrada e, no final, retornar uma lista contendo uma tupla com cor e sua respectiva frequência na imagem.

Por enquanto a função será usada em “counting.py”:

from PIL import Image
from functions import color_value, count_colors

image = Image.open("sample_256x192.png")
counter = count_colors(image)

colors = sorted(
    [
        ("#{:x}{:x}{:x}".format(*(i >> 5 for i in c)), q)
        for c, q in counter
    ],
    key=color_value,
    reverse=True,
)

print("\n".join("{} {:5d}".format(*c) for c in colors))
print("total de cores = {}".format(len(colors)))

Aqui a imagem de exemplo é carregada, a frequência calculada, cores ordenadas de forma decrescente e a relação impressa na tela…

$ python color_count.py
#000000 24020
#e0e0e0  3464
...
#204020     2
#80c0c0     2
Total de cores = 82

Para facilitar a visualização, uma versão ilustrada…

A imagem de exemplo contém 82 cores únicas, logo há 66 cores a mais do que as suportadas pelo modo de vídeo. A solução é bem simples, remover as cores que são mais parecidas até se chegar em algo menor ou igual a 16! 😀

Quantificação de cores

Mas como saber quais cores remover, ou melhor, substituir? O processo em si é chamado de quantização e basicamente o que se tem de fazer é trocar a cor de menor repetição por uma próxima mas que se ocorra mais vezes e daí repetir o processo até alcançar a quantidade de cores desejada.

Mas como calcular a proximidade entre as cores? Considerando que cada cor RGB é uma coordenada dentro de um espaço euclidiano de três dimensões — são os eixos R, G e B mas poderia muito bem ser X, Y e Z — basta usar o cálculo da distância tridimensional entre dois pontos, que é:

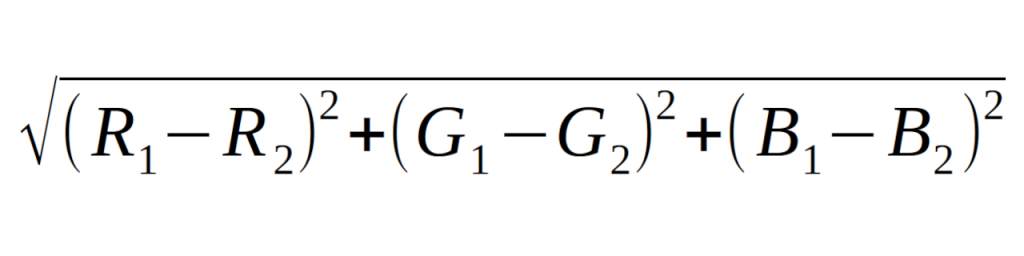
Sim, isto é basicamente uma soma de hipotenusas! Lembra delas? 🙂

Quantificando as cores

Assim o “functions.py” recebe duas novas funções, a primeira para calcular a distância entre as cores (segredo, ela será usada em um outra parte do processo):

from math import sqrt

def distance(origin, destination):

    r1, g1, b1 = origin
    r2, g2, b2 = destination

    return sqrt(
        (r1 - r2) ** 2 + (g1 - g2) ** 2 + (b1 - b2) ** 2
    )

Que recebe duas tuplas contendo a cor em RGB e calcula a distância entre elas.

E outra cuida da quantização das cores propriamente dita:

color_key = lambda color: color[0]

def quantize_colors(palette, length):

    while len(palette) > length:

        palette.sort(key=color_value)

        color, freq = palette.pop(0)
        distances = [
            (idx, distance(color, clr[0]))
            for idx, clr in enumerate(palette[1:], start=1)
        ]

        index, __ = min(distances, key=color_value)

        palette[index] = (
            palette[index][0],
            palette[index][1] + freq,
        )

    return sorted(palette, key=color_key)

Ah sim, o Pillow tem uma função que já faz a quantificação, a quantize(), que executaria o processo até mais rápido mas…

• Não permite que eu reduza o espaço de cores do RGB (trabalha em 24-bit) e
• Ficaria sem saber como funciona o processo de quantificação em si.

O laço principal é executado enquanto o número de cores da paleta for maior que o valor indicado para “length” (neste caso 16). Dentro dele a paleta é ordenada (ordem crescente de frequência), seu primeiro elemento removido, calculada a distância da cor para as demais, recuperado o índice da cor mais próxima, adicionada a frequência da primeira nela e repetido o laço.

Esta rotina é chamada pelo “quantization.py”:

from PIL import Image
from functions import count_colors, quantize_colors

image = Image.open("sample_256x192.png")
colors = count_colors(image)
palette = quantize_colors(colors, 16)

print(
    "\n".join(
        (f"#{r:02x}{g:02x}{b:02x}" for r,g,b in palette)
    )
)

Cujo resultado é a paleta de cores a ser usada na imagem.

$ python quantization.py
#000000
#200000
...
#e0e0c0
#e0e0e0

Ou então de um modo mais visual (apenas as cores)…

E esta é a paleta de cores que será usada para converter a imagem.

Convertendo para 16 cores

A partir deste ponto é possível finalmente converter a imagem para 16 cores, então adiciona-se em “functions.py” duas novas funções:

 FS_NEIGHBORS = (
    (+1, 0, 7),
    (-1, +1, 3), (-1, +1, 5), (+1, +1, 1),
)

def add_noise(bitmap, x, y, error):
    for offset_x, offset_y, debt in FS_NEIGHBORS:
        try:
            off_x, off_y = x + offset_x, y + offset_y
            bitmap[off_x, off_y] = tuple(
                (
                    color + error * debt // 16
                    for color, error in zip(
                        bitmap[off_x, off_y], error
                    )
                )
            )
        except IndexError:
            ...

Que é a mesma rotina da implementação do Floyd-Steinberg usada nas imagens de 256 cores e:

def reduce_colors(image, palette):

    bitmap = image.load()
    colors = {}

    for y in range(image.height, dither=True):
        for x in range(image.width):

            pixel = bitmap[x, y]
            index = colors.get(pixel)

            if index is None:
                index = min(
                    [
                        (idx, distance(pixel, clr))
                        for idx, clr in enumerate(palette)
                    ],
                    key=color_value,
                )[0]
                colors[pixel] = index

            bitmap[x, y] = palette[index]

            if dither:
                error = [
                    old - new
                    for old, new in zip(
                        pixel, palette[index]
                    )
                ]
                add_noise(bitmap, x, y, error)

Assim como a count_colors() ela varre a imagem pixel a pixel, calculando a distância deles para uma das cores disponíveis da paleta, escolhendo a que estiver mais próxima, substituindo-a na imagem. As linhas destacadas dizem respeito a um sistema bem simples de cache que guarda as cores já calculadas e economiza processamento.

No final, caso ‘dither’ seja True, será adicionado um pouco de ruído aos pixels vizinhos.

Uma prévia…

Com tudo agora em seus devidos lugares é possível visualizar o resultado da conversão, mas antes o “reducing.py” para cuidar desta tarefa:

from PIL import Image
from functions import (
    count_colors,
    quantize_colors,
    reduce_colors
}

image = Image.open("sample_256x192.png")
colors = count_colors(image)
palette = quantize_colors(colors, 16)

reduce_colors(image, palette, dither=False)

image.show()

Ele converterá a imagem de exemplo para 16 cores sem aplicar dithering³, daí o color banding, e a exibirá na tela.

(³) A imagem que abre esta publicação é a versão com dithering aplicado.

Fim desta parte

Na próxima parte será a vez de converter a imagem produzida em algo que possa ser visualizado no MSX mas antes de terminar, duas curiosidades…

1. O cache é muito mais eficiente quando o dithering não é aplicado, sendo usado em cerca de 54% das vezes contra 28% quando em uso (lembrando que a adição de erros aumenta o universo de cores na imagem) e
2. Sei que há maneiras mais eficientes e elegantes de fazer a quantificação das cores mas optei por uma que fosse bem fácil de ser explicada (espaço euclidiano, teorema de Pitágoras etc) e, aliás, ela é inspirada na rotina de quantificação de cores em C do livro Morphing Magic escrito por Scott Anderson em 1993.

Claro, os programas (em uma versão bem mais comentada) e imagens utilizadas aqui estão lá no repositório git do blog.